이번 장에서는 자료구조의 정의와 자료구조의 기본형인 배열에 대해 알아보았다.
배열은 그동안 공부했었던 모든 책에서 한번 이상은 다뤄보았기 때문에 개념에 대해서는 쉽게 이해할 수 있었지만 배열의 알고리즘이 나온 이후로 머리가 너무 아프다.
나는 문제를 먼저 내가 한번 풀어보고 책에서는 어떻게 풀었는지 내 코드와 비교해가며 공부하고있는데 정말 내가 생각하지 못했던 방법이 이렇게 많고 내가 만든 코드는 정말 초라하다는 생각이 많이 들었다.
빨리 실력이 늘어 어려운 알고리즘 문제도 쉽게 풀 수 있는 안목이 생겼으면 좋겠다.
1. 자료구조와 배열
자료구조란 여러개의 값을 하나의 변수 안에 저장해 놓을 수 있어서 코드를 쉽고 효율적으로 작성할 수 있다. 대표적인 자료구조의 형태는 배열이 있다.
배열은 변수의 개수를 확실히 줄여주는 효과가 있다. 예를 들어 여러 학생의 성적을 받는 프로그램이 있다고 치자.
이 때 학생의 수만큼 변수를 만드는 것은 용량과 효율성 모두 좋지 않지만 하나의 배열을 이용하여 모든 학생의 성적을 담는다면 코드를 알아보기 쉽고 효율적으로 만들 수 있다.
score_list = []
count = 1
def ave(li: list):
a = sum(li) / (len(li) - 2)
return a
while (1):
score = int(input(f'{count}번 학생의 점수 입력 : '))
score_list.append(score)
count += 1
if -999 in score_list:
score_list.append(999)
print('총점 : ', sum(score_list))
print('평균 : ', ave(score_list))
break내가 만들어 본 학생 성적 입력 프로그램이다. 무한 반복문을 만들어 학생의 수를 모르더라도 입력을 계속 할 수 있고 -999를 입력했을 때 멈추는 프로그램이다.
1-1. 배열
배열의 대표적인 예시는 리스트와 튜플이다. 리스트란 파이썬이 제공하는 배열이고 튜플은 원소에 순서를 매겨 결합한 것으로 원소를 변경할 수 없는 이뮤터블 자료형이다.
문제1. 배열의 최댓값 구하기
def maximum(li):
max = li[0]
for i in range(len(li)):
if li[i] > max:
max = li[i]
return max
if __name__ == '__main__':
print('배열의 최댓값을 구합니다')
num = int(input('원소 수를 입력하시오 : '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]값을 입력하시오 : '))
print((f'최댓값은 {maximum(x)}입니다.'))이 문제는 max() 함수 내부에서 일어나는 알고리즘에 대한 문제이다. 순서도를 본다면 아래의 그림과 같다.
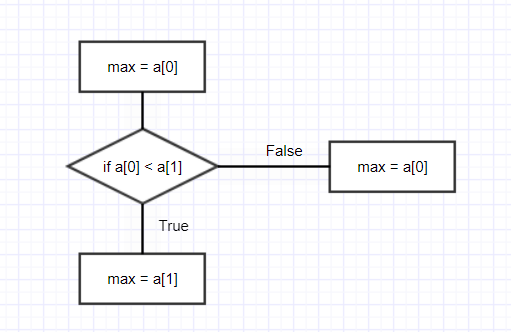
이렇게 리스트의 원소를 0번부터 i번까지 크기를 비교해보며 max 변수에 저장하는 알고리즘이다.
문제 1-2. End를 입력하면 종료하기
from test import maximum
print('배열의 최댓값을 구합니다.')
print('END를 입력하면 종료합니다.')
num = 0
x = []
while (1):
s = input(f'x[{num}]원소 입력:')
if s == 'END':
break
x.append(int(s))
num += 1
print(f'{num}개 입력')
print(f'최댓값은 {maximum(x)}')이 코드는 이전에 사용했던 maximum 함수를 불러온 코드이다. 그걸 이용해 간단한 코드를 만들어 보았다.
문제2. 배열 원소를 역순으로 정렬하기
def rev (a):
n = len(a)
for i in range(n // 2):
a[i],a[n - i - 1] = a[n - i - 1],a[i]
if __name__ == '__main__':
print('배열 원소를 역순으로 정렬')
nx = int(input('원소 수 입력 :'))
x = [None] * nx
for i in range(nx):
x[i] = int(input(f'x[{i}]값을 입력 :'))
rev(x)
for i in range(nx):
print(f'x[{i}] = {x[i]}')내가 배열의 원소를 역순으로 정렬하기 위한 방법을 생각해보았다. 먼저 i가 0부터 리스트의 끝번호까지라고 가정했을 때 a[i] 와 a[끝번호 - i] 를 교환하면 된다고 생각하며 작성했다.
문제3. 진수 변환하기
def card_conv(x:int,r:int) -> str:
d = ''
dchar = '01234567890ABCDEFGHIJKLMNOPQRSTUVWXYZ'
while x > 0:
d += dchar[x % r]
x //= r
return d[::-1]
if __name__ == '__main__':
while(True):
while(True):
no = int(input('변환할 값으로 음이 아닌 정수를 입력하세요 : '))
if no > 0:
break
while(True):
cd = int(input('어떤 진수로 변환할까요 ?'))
if 2 <= cd <= 36:
break
print(f'{cd}진수로는 {card_conv(no,cd)}입니다.')
retry = input('ㄹ?(Y/N)')
if retry in {'N','n'}:
break
이 코드를 이해하려면 진수를 변환하는 방법 먼저 알아야한다. 예를 들어 33을 2진수로 변환한다면 33을 2로 소인수 분해를 하고 순서대로 나온 수를 역순으로 나열하면 진수변환이 끝난다.
이 때 dchar에 0부터 z까지 문자열을 나열해 진수변환에 필요한 문자를 가져오는 식으로 완성된다. 사실 말로 풀어서 하기 어려우니 코드를 한 줄 씩 보는게 가장 이해가 쉬울 거라고 생각한다.
문제 4. 1000까지의 소수 나열 (1)
# 1000 이하의 소수 나열하기
counter = 0
for i in range(2,1001):
for j in range(2,i):
counter += 1
if j % i == 0:
break
else :
print(i)
print(f'나눗셈을 실행한 횟수{counter}')문제 4-1. 1000까지의 소수 나열 (2)
# 알고리즘 개선
counter = 0
ptr = 0
prime = [None] * 500
prime[ptr] = 2
ptr += 1
for i in range(3,1001,2):
for j in range(1,ptr):
counter += 1
if i % prime[j] == 0:
break
else:
prime[ptr] = i
ptr += 1
for k in range(ptr):
print(prime[k])
print(f'나눗셈을 실행한 횟수{counter}')문제 4-2. 1000까지의 소수 나열 (3)
# 알고리즘 개선 2
count = 0
ptr = 0
prime = [None] * 500
prime[ptr] = 2
ptr += 1
prime[ptr] = 3
ptr += 1
for n in range(5,1001,2):
i = 1
while prime[i] * prime[i] <= n:
count += 2
if n %prime[i] == 0:
break
i += 1
else:
prime[ptr] = n
ptr += 1
count += 1
for i in range(ptr):
print(prime[i])
print(f'횟수 : {count}')첫번째 문제의 알고리즘은 모든 수를 대입해 나누어보는 것이다. 이렇게 한다면 계산은 매우 많아지겠지만 확실하다는 장점이 있다. 총 계산 횟수는 78022 이다.
하지만 두번째 알고리즘의 경우에는 이미 짝수는 모두 소수가 아니라는 것을 알고있기 때문에 짝수는 계산에 포함하지 않는다. 이렇게 함으로써 계산횟수가 현저히 줄어들게 된다. 총 계산 횟수는 14622이다.
마지막 알고리즘은 짝수만을 계산하는 것을 유지하되 예를 들어 5로 나누어지는 수라면 5의 제곱은 모두 나누어 질 거라는 점을 이용해 미리 계산식에서 제외하는 방법이다.
그래서 총 계산 횟수는 3774로 처음 계산 횟수보다 매우 큰 차이를 보여준다.
'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 검색 알고리즘 - (이진 검색) (0) | 2022.07.22 |
|---|---|
| 검색 알고리즘 - (선형 알고리즘) (0) | 2022.07.21 |
| 반복하는 알고리즘 (2) (0) | 2022.07.18 |
| 반복하는 알고리즘 (1) (1) | 2022.07.15 |
| 알고리즘이란? (0) | 2022.07.15 |
