하노이의 탑
하노이의 탑은 큰 원판이 작은 원판 위로 올 수 없다는 규칙을 가지고 있으며 모든 원판을 지정한 기둥으로 옮기면 되는 문제이다.
이 문제의 해결법은 아래 그림과 같이 가장 큰 원판을 제외한 모든 원판을 2번째 기둥에 놓고 가장 큰 원판을 목표 기둥에 놓으면 된다.
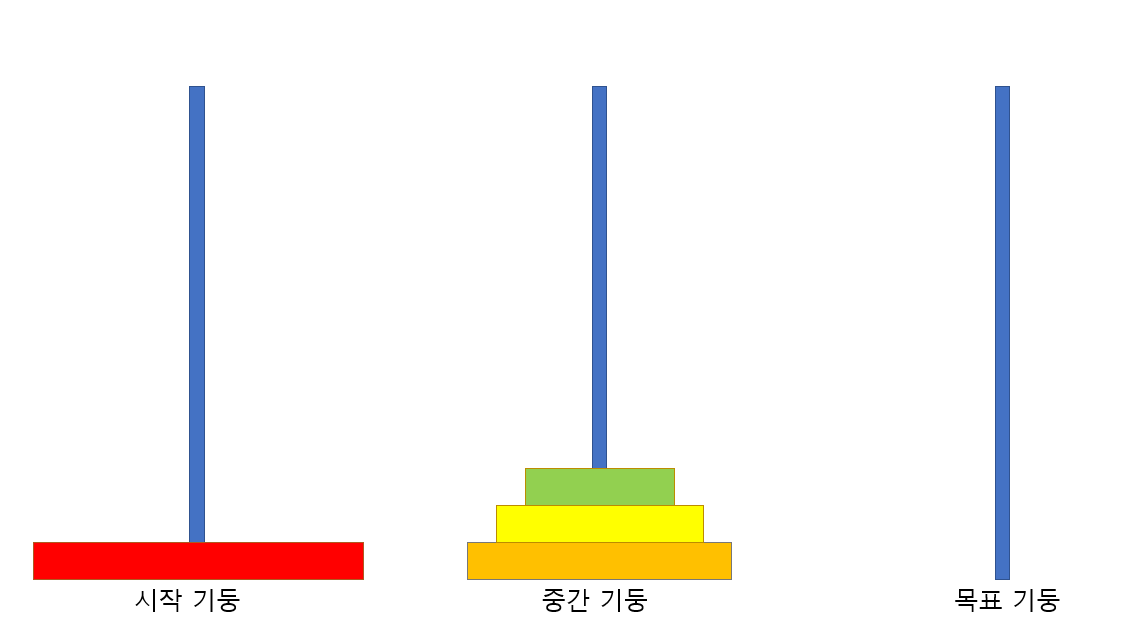
그렇게 된다면 중간 기둥에 큰 원판을 제외한 다른 원판을 쌓는 과정이 문제가 된다. 하지만 다시 생각해보면 이 과정도 중간 기둥을 목표 기둥이라 놓고 가장 큰 원판을 목표기둥(2번째 기둥) 에 놓기만 하면 된다.
이렇게 점차 줄여나가면 결국 하노이의 탑 문제를 풀 수 있는 것이다.
아래는 하노이의 탑 코드이다.
def move (no, start, target):
if no > 1:
move(no - 1, start, 6 - start - target)
print(f'원반{no}를 {start} > {target}으로 옮김.')
if no > 1:
move(no - 1, 6 - start - target, target)
n = int (input('원반의 개수 입력 : '))
move(n,1,3)사실 중간 기둥을 구하는 수식이 왜 6 - x -y인지는 아직도 잘 모르겠다. 책에는 기둥 번호의 합이 6이므로 시작기둥, 목표기둥이 어디에 있던 중간 기둥을 구할 수 있다고 써있는데 잘 이해가 가질 않는다.
하지만 코드를 읽어보며 전체적인 코드 구현이 어떻게 되는지에 대한 이해는 충분히 된 것 같다.
8퀸문제
8퀸문제는 8 x 8 인 체스판에 8개의 퀸을 서로를 공격하지 못하도록 놓는 문제이다. 직선과 대각선을 모두 고려해야하기 때문에 생각보다 복잡했고 어려웠다.
먼저 아무런 조건 없이 퀸을 배치한다면 64 * 63 * 62 * 61 * ... * 57 = 매우 큰 수가 나온다.
규칙 1. 각 열에 퀸을 1개씩만 배치해야한다.
규칙 2. 각 행에 퀸을 1개씩만 배치해야한다.
규칙 3. 대각선에 퀸을 1개씩만 배치해야한다.
이제 각 열에 퀸을 1개씩만 배치해야한다는 규칙을 적용해본다면 8 ^ 8 가지의 경우의 수가 나온다.
pos = [0] * 8
def put() -> None:
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
for j in range(8):
pos[i] = j
if i == 7:
put()
else:
set(i + 1)
set(0)
다음은 규칙 2를 적용한 코드이다.
pos = [0] * 8
flag = [False] * 8
def put() -> None:
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
for j in range(8):
if not flag[j]:
pos[i] = j
if i == 7:
put()
else:
flag[j] = True
set(i + 1)
flag[j] = False
set(0)다음은 모든 규칙을 적용한 코드이다.
pos = [0] * 8
flag = [False] * 8
flag_a = [False] * 15
flag_b = [False] * 15
def put() -> None:
"""각 열의 배치한 퀸의 위치를 출력"""
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
"""i열에 퀸을 배치"""
for j in range(8):
if(not flag[j] and not flag_a[i+j] and not flag_b[i-j+7]):
pos[i] = j #퀸을 j행에 배치
if i == 7: #모든 열에 퀸 배치를 종료
put()
else:
flag[j] = flag_a[i+j] = flag_b[i-j+7] = True
set(i+1) #다음 열에 퀸을 배치
flag[j] = flag_a[i+j] = flag_b[i-j+7] = False
set(0) #퀸을 0열에 배치
'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 정렬 알고리즘 (2) - 셸정렬, 퀵정렬 (0) | 2022.07.30 |
|---|---|
| 정렬 알고리즘 (1) - 버블정렬, 단순 선택/삽입 정렬 (0) | 2022.07.28 |
| 재귀 알고리즘 (1) (0) | 2022.07.27 |
| 스택과 큐 (0) | 2022.07.25 |
| 검색 알고리즘 - (해시법) (0) | 2022.07.24 |




댓글