정렬 알고리즘은 정수의 배열을 오름/ 내림차순으로 정렬하기에 최적화 된 방법을 찾는 방식이다.
따라서 대소비교하는 수를 최소화 하는데에 초점을 두기 때문에 수식이 많아 코드를 이해하기 어려웠고 복잡했다. 유사한 방법의 알고리즘도 있어서 둘의 차이를 헷갈릴 때도 있었지만 그 속에서도 다른 점이 많았다.
정말 알고리즘이 늘기 위해선 문제를 많이 보고 직접 풀어보는 방법밖에는 없는 것 같다.
정렬 알고리즘
정렬이란 항목값의 대소에 따라 데이터 집합을 일정한 수서로 나열하는 작업이다. 값이 작은 데이터를 앞에 놓는것을 오름차순, 값이 큰 데이터를 앞에 놓는 것을 내림차순이라고 한다.
버블정렬
버블정렬은 이웃한 두 원소의 대소관계를 비교하여 교환을 반복하는 알고리즘이다. 총 대소구분을 하는 횟수는 (n - 1) + (n - 2) + (n - 3) + ... + (n - m이 1이 되는 값) 까지이며 시간복잡도는 O(n^2)이다.
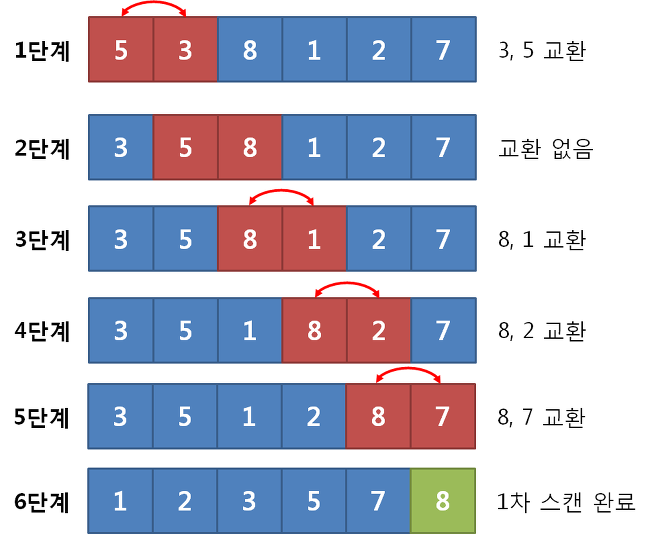
버블정렬 프로그램
def bubble(a):
n = len(a)
for i in range(n - 1):
for j in range(n - 1, i, -1):
if a[j - 1] > a[j]:
a[j - 1], a[j] = a[j], a[j - 1]
print(a)
my_list = [4, 5, 6, 2, 5, 1, 3, 7, 9]
print(bubble(my_list))단순 선택 정렬
단순 선택정렬은 배열의 가장 작은 값을 찾아 인덱스의 0번부터 끝까지 채워나가는 것이다. 따라서 시간복잡도는 위의 버블정렬과 같이 O(n^2)이 된다.
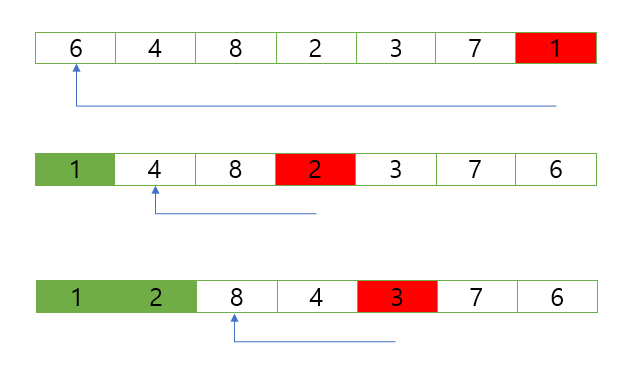
다음은 단순 선택정렬의 코드이다.
def selection_sort(a: list):
n = len(a)
for i in range(n - 1): # n - 1번의 계산이 끝나면 남은 마지막 자리에는 가장 큰 수가 들어갈 수 밖에 없음
min = i
for j in range(i + 1,n):
if a[j] < a[min]: # min에 들어가 있는 수보다 다음 인덱스에 있는 수가 더 작다면
min = j
a[i], a[min] = a[min], a[i]
print('a :',a)
print('min :',min)
a_list = [1,5,3,6,7,2,8,9]
print(selection_sort(a_list))
단순 삽입 정렬
단순 삽입정렬은 주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘이다.
처음에는 버블정렬과 헷갈렸었는데 버블정렬은 서로 이웃한 두 원소의 값만 비교하는 것이고 단순 삽입정렬은 왼쪽 인덱스와 비교했을 때 크기가 작을 시 계속해서 왼쪽 인덱스와 비교한다.
자신보다 작은 값이 나오기 전까지 비교하여 왼쪽으로 이동하기때문에 결국에는 자기 위치를 찾게된다.
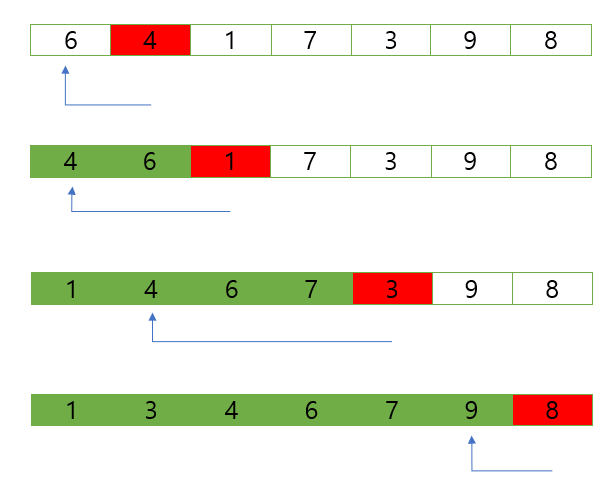
다음은 단순 삽입 정렬 알고리즘의 코드이다.
def insertion_sort(a: list):
n = len(a)
for i in range(1, n):
j = i
tmp = a[i]
while j > 0 and a[j - 1] > tmp:
a[j] = a[j - 1]
j -= 1
a[j] = tmp
print('tmp: ', tmp)
print('a: ', a)
a_list = [3, 4, 5, 1, 9, 6, 7]
print(insertion_sort(a_list))위의 소개한 3가지의 알고리즘은 모두 시간복잡도가 O(n^2) 이므로 좋지 않은 알고리즘이다. 다음 글에 포스팅할 알고리즘은 개선된 알고리즘으로 모두 시간 복잡도가 좋은 편에 속한다.
'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 정렬 알고리즘 (3) - 병합정렬, 힙정렬 (0) | 2022.08.03 |
|---|---|
| 정렬 알고리즘 (2) - 셸정렬, 퀵정렬 (0) | 2022.07.30 |
| 재귀 알고리즘 (2) - (하노이의 탑, 8퀸 문제) (0) | 2022.07.27 |
| 재귀 알고리즘 (1) (0) | 2022.07.27 |
| 스택과 큐 (0) | 2022.07.25 |
