지금까지 여러 검색 알고리즘을 배우며 그동안 배웠던 방법이 헷갈리기 시작했다. 그래서 지금까지 배웠던 내용을 다시 한 번 복습해봤다.
위 세가지 알고리즘은 간단하지만 비교적 좋지 못한 알고리즘이고 아래 알고리즘은 복잡하지만 효율적인 알고리즘이다.
버블정렬
: 두 이웃한 원소끼리 대소 비교 반복
단순 선택 정렬
: 배열의 가장 작은값을 0번 인덱스부터 채워나가는 것
단순 삽입 정렬
: 배열의 1번 인덱스를 기준으로 왼쪽의 (작은쪽) 값과 비교해나가며 맞는 자리를 찾아가는 방법
셸정렬
: 단순 삽입 정렬의 상위호환. 배열의 몇 칸 이라는 기준을 두어 값을 비교해 미리 어느정도 정렬을 해놓음
퀵정렬
: 피벗값을 기준으로 배열을 나누어 배열의 인덱스가 1개밖에 없을 때 까지 나눈 후 병합한다.
병합정렬
: 배열의 중간을 나누어 병합한다. 퀵정렬과 비슷하지만 h값을 나누는 기준이 다르기 때문에 시간 차이가 난다.
힙정렬
: 이진트리를 만들어 부모 원소는 항상 자식보다 커야한다. 가장 큰 부모 (루트)를 배열의 맨 뒤에 놓음으로써 배열을 정렬함
하지만 내가 느낀 점은 아래에 있는 효율적인 알고리즘은 모두 위의 세가지 알고리즘을 보완하거나 기초로 둔 알고리즘이라는 것이다.
문제를 해결하기 위해 처음부터 어려운 방법을 생각하기보단 가장 쉬운 방법을 떠올리며 그 방법을 보완해가는 방식으로 천천히 발전해가는 것이 좋은 자세라고 생각한다.
병합정렬
병합정렬을 공부하며 퀵정렬과 유사한것 같아 많이 헷갈렸었다.
하지만 다시 퀵정렬을 정확히 공부한 후에 병합정렬은 배열의 인덱스의 중간을 자르는 방식으로 나누지만 퀵정렬은 배열의 값의 중간값으로 나눈다는 점에서 다르다는 것을 알았다.
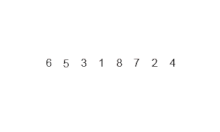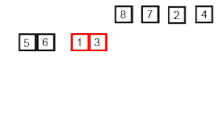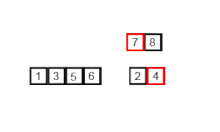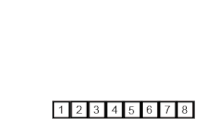
병합정렬도 퀵정렬과 마찬가지로 배열의 인덱스가 1이 될 때까지 나누기 떄문에 재귀적이다. 다음은 오름차순으로 나열된 두 배열을 병합정렬로 정렬하는 코드이다.
def merge_sorted_list(a, b, c):
pa, pb, pc = 0, 0, 0 # 커서 초기화
na, nb, nc = len(a), len(b), len(c)
while pa < na and pb < nb: # a,b 커서가 해당 리스트 안에 있다면
if a[pa] <= b[pb]: # a 커서가 b 커서보다 작다면
c[pc] = a[pa]
pa += 1
else :
c[pc] = b[pb]
pb += 1
pc += 1
while pa < na:
c[pc] = a[pa]
pa += 1
pc += 1
while pb < nb:
c[pc] = b[pb]
pb += 1
pc += 1
if __name__ == '__main__':
a_index = int(input('a 리스트의 원소 수 입력 : '))
b_index = int(input('b 리스트의 원소 수 입력 : '))
a = []
b = []
c = [None] * (a_index + b_index)
for i in range(a_index):
a_num = input('a 리스트의 원소 입력 : ')
a.append(a_num)
for i in range(b_index):
b_num = input('b 리스트의 원소 입력 : ')
b.append(b_num)
print('정렬을 마칩니다.')
print('a : ',a)
print('b : ', b)
print('c : ', c)
merge_sorted_list(a,b,c)
print(f'배열 a : {a}')
print(f'배열 b : {b}')
print(f'배열 c : {c}')위 코드는 한번만 병합하기때문에 두 리스트 모두 정렬되어있어야한다.
다음은 정렬되어있지않은 리스트를 재귀적으로 여러번 나누어 병합한 병합정렬의 코드이다.
def merge_sort(a):
n = len(a)
buff = [None] * n
def _merge_sort(a,left: int,right: int):
if left < right:
center = (left + right) // 2
_merge_sort(a, left, center)
_merge_sort(a, center + 1, right)
p = j = 0
i = k = left
while i <= center:
buff[p] = a[i]
p += 1
i += 1
while i <= right and j < p:
if buff[j] <= a[i]:
a[k] = buff[j]
j += 1
else :
a[k] = a[i]
i += 1
k += 1
while j < p:
a[k] = buff[j]
k += 1
j += 1
_merge_sort(a, 0, n - 1)
print('buff : ',buff)
del buff
if __name__ == '__main__':
print('병합정렬을 수행')
num = int(input('원소 수 입력 : '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
merge_sort(x)
print('오름차순으로 정렬')
for i in range(num):
[print(f'xx[{i}] = {x[i]}')]힙정렬
힙정렬은 이진트리를 기초로 한 정렬 알고리즘이다. 이 때 트리란 부모와 자식간의 대소관계가 항상 성립하는 것을 트리라고 한다.
하지만 힙은 형제 사이의 대소관계가 일정하지 않기때문에 부분 순서 트리라고도 한다. 트리에서 가장 큰 부모를 루트라고 하며 루트를 배열의 마지막에 추가하는 형식으로 정렬이 진행된다.
이 때 힙의 위에서 아래로 왼쪽부터 오른쪽 순서로 배열이 만들어지는데 사진과 같다.
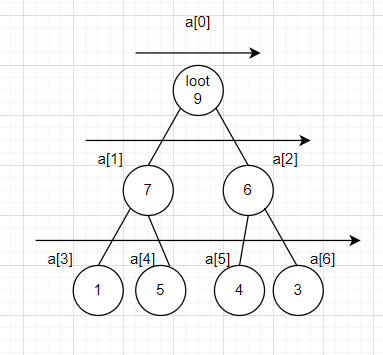
이 때 원소의 부모 혹은 왼쪽 오른쪽 자식이 몇 번 인덱스인지 알기 위해서는 다음 공식을 이용할 수 있다.
원소 a[ i ]일 때
부모 : a [(i - 1) // 2]
왼쪽 자식 : a [ i *2 + 1]
오른쪽 자식 : a [ i * 2 + 2]
원소 1번인 7을 예시로 들자면 부모는 0번 원소인 9가 될 것이고 왼쪽자식은 a [3]인 1 오른쪽 자식은 a [4] 인 5가 될 것이다.
루트를 삭제한 힙의 재구성
힙정렬에서 루트는 가장 큰 값이라고 했다. 가장 큰 값을 리스트에 마지막으로 넣어둔 후 그 뒤로 가장 큰 값을 찾는 순서는 다음과 같다.
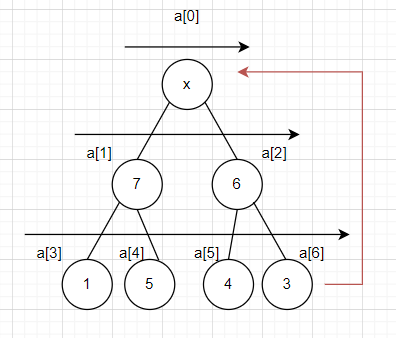
- 가장 마지막 원소인 3을 루트에 위치시킨다.
- 자식중에 더 큰 원소와 자리를 교환한다.
- 이를 반복한다.
다음은 힙정렬의 코드이다.
from typing import MutableSequence
def heap_sort(a: MutableSequence):
def down_heap(a: MutableSequence, left: int, right: int):
temp = a[left]
parent = left
while parent < (right + 1) // 2:
cl = parent * 2 + 1
cr = cl + 1
child = cr if cr <= right and a[cr] > a[cl] else cl
if temp >= a[child]:
break
a[parent] = a[child]
parent = child
a[parent] = temp
n = len(a)
for i in range((n - 1) // 2, -1, -1):
down_heap(a, i, n - 1)
for i in range(n - 1, 0, -1):
a[0], a[i] = a[i], a[0]
down_heap(a, 0, i - 1)
if __name__ == '__main__':
print('힙정렬을 수행합니다.')
num = int(input('원소 수 입력 : '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
heap_sort(x)
print('오름차순으로 정렬했습니다.')
for i in range(num):
print(f'x[{i}] = {x[i]}')
'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 문자열 검색 알고리즘 (0) | 2022.08.04 |
|---|---|
| 정렬 알고리즘 (fin) - 도수정렬 (0) | 2022.08.03 |
| 정렬 알고리즘 (2) - 셸정렬, 퀵정렬 (0) | 2022.07.30 |
| 정렬 알고리즘 (1) - 버블정렬, 단순 선택/삽입 정렬 (0) | 2022.07.28 |
| 재귀 알고리즘 (2) - (하노이의 탑, 8퀸 문제) (0) | 2022.07.27 |




댓글