이번 단원은 검색 알고리즘 중 이전에 배웠던 숫자가 아닌 문자를 검색하는 내용이다.
나는 이전에 배웠었던 숫자의 검색 알고리즘을 떠올리며 문자를 모두 유니코드로 변환해 해시 법이나 선형 알고리즘으로 검색하는 줄 알았는데 내가 생각했었던 내용과는 다르게 문자 그대로를 비교하는 방법이었다.
따라서 수를 검색하는 알고리즘에서 선형 알고리즘이 문자열에서는 브루트 포스 법과 유사하다는 것도 알 수 있었다.
브루트포스법
앞서 말했듯이 숫자를 검색하는 가장 기초적인 알고리즘이 선형 알고리즘이라면 문자를 검색하는 알고리즘은 브루트 포스이다.
이때 찾으려는 문자열을 패턴이라 하고 검색되는 쪽의 문자열을 텍스트라고 한다. 브루트포스법의 원리는 다음과 같다.
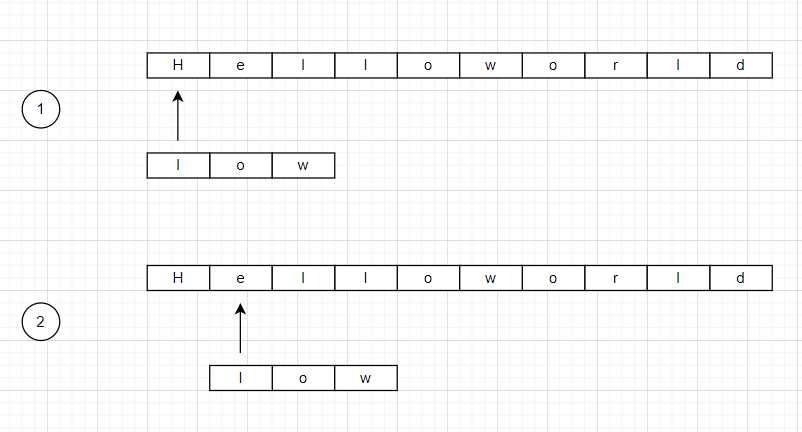
텍스트와 패턴을 대조하여 첫 번째 문자가 같지 않으면 오른쪽으로 한 칸씩 이동하는 형식이다.
실행코드는 다음과 같다.
def bf_match(txt: str, pat: str) -> int:
pt = 0 # txt의 커서
pp = 0 # pat의 커서
while pt != len(txt) and pp != len(pat): # 커서가 문자열 안에 있을 때
if txt[pt] == pat[pp]: # 텍스트와 패턴의 문자가 같다면
pt += 1
pp += 1
else :
pt = pt - pp + 1
pp = 0
return pt - pp if pp == len(pat) else - 1
if __name__ == '__main__':
s1 = input('텍스트 입력 :')
s2 = input('패턴을 입력 :')
idx = bf_match(s1,s2)
if idx == -1:
print('텍스트 안에 패턴이 존재하지 않습니다.')
else :
print(f'{[idx + 1]}번째 문자가 일치합니다.')kmp법
kmp 법은 브루트포스법에서 조금 더 발전한 알고리즘이다. 이미 이전에 검사한 결과값을 이용해 값이 틀렸을 때 패턴의 이동을 최대화 하는 기법이다,
예를 들자면 텍스트가 '가나가나가나가가' 일 때 패턴이 '가나가가'라고 해보자.
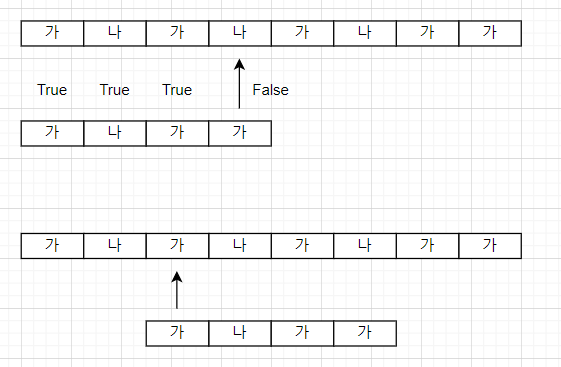
이 때 틀리더라도 바로 다음 문자가 아닌 '가'라는 문자까지 넘어갈 수 있다. 따라서 kmp법에서는 값을 저장해야하기 때문에 새로운 배열이 필요하다.
다음은 kmp법의 실행코드이다.
def kmp_match(txt: str, pat: str):
pt = 1
pp = 0
skip = [0] * (len(pat) + 1)
skip[pt] = 0
while pt != len(pat):
if pat[pt] == pat[pp]:
pt += 1
pp += 1
skip[pt] = pp
elif pp == 0:
pt += 1
skip[pt] = pp
else :
pp = skip[pp]
pt = pp = 0
while pt != len(txt) and pp != len(pat):
if txt[pt] == pat[pp]:
pt += 1
pp += 1
elif pp == 0:
pt += 1
else :
pp = skip[pp]
return pt - pp if pp == len(pat) else -1
if __name__ == '__main__':
s1 = input('텍스트 입력 :')
s2 = input('패턴 입력 :')
idx = kmp_match(s1,s2)
if idx == - 1:
print('텍스트 안에 패턴이 존재하지 않습니다.')
else :
print(f'{[idx + 1]}번째 문자가 일치합니다.')보이어/무어법
보이어/ 무어법은 다른 알고리즘보다 효율이 훨씬 뛰어나 실제로 많이 사용하는 알고리즘이다. 이 알고리즘의 특징은 패턴의 마지막 문자를 텍스트에 대조해 본다는 것이다.
따라서 패턴의 오른쪽부터 왼쪽으로 대조가 이루어지고 만약 문자가 일치하지 않는다면 패턴의 길이만큼 패턴을 이동할 수 있다.
또한 일치하지 않을 때 kmp알고리즘과 마찬가지로 skip 테이블을 만드는데 이 테이블은 문자가 일치하지 않을 때 오른쪽으로 얼만큼 이동할지를 미리 테이블로 정해놓는 역할을 한다.
테이블이 패턴의 이동량을 결정하는 경우
- 패턴에 포함되지 않는 문자를 만난 경우
패턴의 크기만큼 이동
- 패턴에 포함되는 문자를 만난 경우
마지막에 나오는 위치의 인덱스가 k 일때 이동량은 n - k - 1 이다. 하지만 같은 문자가 패턴안에 중복해서 존재하지 않으면 패턴의 맨 끝 문자의 이동량은 n
보이어/무어법의 코드는 다음과 같다.
def bm_match(txt, pat):
skip = [None] * 256
for pt in range(256):
skip[pt] = len(pat)
for pt in range(len(pat)):
skip[ord(pat[pt])] = len(pat) - pt - 1
while pt < len(txt):
pp = len(pat) - 1
while txt[pt] == pat[pp]:
if pp == 0:
return pt
pt -= 1
pp -= 1
pt += skip[ord(txt[pt])] if skip[ord(txt[pt])] > len(pat) - pp \
else len(pat) - pp
return -1
if __name__ == '__main__':
s1 = input('텍스트 입력 :')
s2 = input('패턴 입력 : ')
idx = bm_match(s1, s2)
if idx == -1:
print('텍스트 안에 패턴이 존재하지 않습니다.')
else:
print(f'{(idx + 1)}번째 문자가 일치합니다.')'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 커서를 이용한 연결 리스트 (0) | 2022.08.07 |
|---|---|
| 포인터를 이용한 연결 리스트 (0) | 2022.08.05 |
| 정렬 알고리즘 (fin) - 도수정렬 (0) | 2022.08.03 |
| 정렬 알고리즘 (3) - 병합정렬, 힙정렬 (0) | 2022.08.03 |
| 정렬 알고리즘 (2) - 셸정렬, 퀵정렬 (0) | 2022.07.30 |
