이번 책에서는 먼저 1장에서 코딩테스트의 기본에 대해 다루고 그 후에 파이썬, 3장부터 자료구조가 나와 책을 시작한지 조금 되었는데도 알고리즘이라는 카테고리에 맞지 않아 블로그 작성이 더뎌졌다.
하지만 이번 장 이후부터는 자료구조와 알고리즘 모두 계속 나오기 때문에 블로그 업로드 속도가 조금 빨라질 것 같다.
빅오 (Big-O)
: 알고리즘의 효율성을 표기하는 표기법. 보통 알고리즘의 시간 복잡도(얼마나 빠른지) 와 공간 복잡도(메모리가 얼마나 사용되는지) 를 나타내는데 사용된다.
→ 입력값이 무한에 수렴할 때 (최악의 경우)알고리즘의 시간/공간 복잡도를 표기한다.
다음은 알고리즘의 효율성이 좋은 순서대로 나열한 빅오 표기법 이다.
- O (1) : 최상의 알고리즘이다. 입력값이 무한이더라도 항상 같은 시간이 소요된다.
- O (log n) : 로그 n 은 입력값이 크더라도 영향이 심하지 않다.
- O (n) : 입력값과 효율성이 1:1로 비례하는 알고리즘이다. 이러한 알고리즘을 선형시간 알고리즘이라고 하며 모든 입력값을 한번은 확인해야 한다.
- O (n log n) : 대부분의 효율이 좋은 알고리즘이 이에 해당한다. 복잡한 알고리즘의 경우 위의 3가지가 나오기 힘든데 이 단계는 어려운 문제를 효율성 있게 잘 풀었다면 충분히 나올 수 있는 단계이다. 입력값이 최선인 경우 O(n)이 될 수도 있다.
- O (n^2) : n^2 부터 입력값이 커질수록 시간복잡도가 크게 증가한다.
- O (2^n) : n^2와 혼동하기 쉬운데 둘의 차이는 어마어마하게 크다. 2^n이 훨씬 더 큰 값을 가지고 있기 때문에 입력값이 커지면 시간은 기하급수적으로 늘어난다.
자료구조는 크게 메모리 공간 기반의 연속/ 연결로 구별된다. 그 중 연속 방식의 가장 대표적인 예시는 우리가 흔히 알고있는 배열이다. 파이썬에서는 배열을 list 로 사용하고 이는 동적 배열에 해당한다.
배열
: 값 또는 변수 엘리먼트의 집합으로 구성된 구조. 하나 이상의 인덱스 혹은 키로 식별된다.
→ 크기가 고정되어 있으며 한번 생성한 배열은 크기를 변경하는 것이 불가능
→ 어느 위치에나 O(1)에 조회가 가능하다.
동적 배열
: 배열의 단점을 보완한 것. 실제 데이터의 크기를 가늠하기 어렵기 때문에 배열의 크기 고정이라는 점이 매우 불편할 수도 있는데 이를 보완한 배열이다.
크기를 지정하지 않아도 배열의 크기가 원소에 맞게 커지기 때문에 여러 언어가 지원한다. ex) 파이썬의 list
문제 1. 덧셈을 이용하여 타겟을 만들 수 있는 두 인덱스를 반환하라.
- 입력
num = [7, 2, 11, 15], target = 9- 출력
[0, 1]
브루트 포스
: 모든 경우의 수를 탐색한다. 그렇기 때문에 언젠가는 분명히 문제를 풀 수 있겠지만 효율성을 중요시 하는 알고리즘에서는 매우 비효율적이다. 이 경우의 시간 복잡도는 O(n^2) 이며 조금 더 최적화 되는 방법을 찾아야한다.
def twosum(self,nums,target):
for i in range (len(nums)):
for j in range (i+1,len(nums)):
if nums[i] + nums[j] == target:
return [i, j]
타겟에서 첫번째 수를 뺀 결과 키 조회
: 이 방법은 정말 내가 생각하지도 못했었다. 알고나니 이걸 왜 몰랐을까 하는 생각이 들었을 정도로 쉬운 방법이지만 이런 발상의 전환이 알고리즘 공부에 있어서 필요한것 같다.
def twosum(nums, target):
nums_map = {}
for i, num in enumerate(nums):
nums_map[num] = i
for i, num in enumerate(nums):
if target - num in nums_map and i != nums_map[target - num]:
return [i, nums_map[target - num]]
print(twosum([1,5,6,8,7,2,6,4,7,9],10))나는 이 문제에 추가하여 타겟값을 만들 수 있는 가장 빠른 값을 찾기보다는 타겟값을 만들 수 있는 모든 수를 찾는 코드도 짜보았다.
def twosum(nums, target): #가장 빠른 하나의 경우의 수
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[i] + nums[j] == target:
return [i, j]
def my_twosum(nums : list[int],target) -> list: # 모든 경우의 수
return_list = []
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[i] + nums [j] == target:
return_list.append([i,j])
return return_list
print(twosum([3,5,1,6,3,7,2,7,9],5))
print(my_twosum([3,5,1,6,3,7,2,7,9,2,2,2,2,2],5))
문제2. 빗물 트래핑
- 입력
[0,1,0,2,1,0,1,3,2,1,2,1]- 출력
6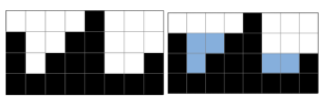
문제는 입력한 값이 박스의 높이가 되고 그 안에 물이 얼마나 담길 수 있는지에 대한 값을 반환해야하는 문제이다.
가장 먼저 내가 생각한 방법은
1. list 가 [a,b,c,d,e,f,g] 일 때 a가 b보다 크다면 a값을 max_left에 저장시키고 그 뒤로 a보다 같거나 큰 값을 찾는다.
2. 예를 들어 c가 a보다 크거나 같다면 a와 c 두 값을 비교해 더 작은값을 b와 뺀다.
3. 두 수의 차가 b에 담길 수 있는 물이니 rain 변수에 추가한다.
이 방법으로 코드를 짜봤는데 정말 이론과 실전은 다르다는걸 깨달았다. 몇시간동안 고민해도 풀리지 않아서 우선 지금까지 했던 내용을 올리고 내 실력이 조금 더 향상되면 다시 보완할 예정이다.
# 빗물을 담아보자 !
def raining(block: list[int]):
block_list = len(block)
ans_block = []
rain = 0
for i in range(0, block_list - 1):
if block[i] > block[i + 1]: # a블록이 b 블록보다 크다면 (물이 담길 수 있다면)
for j in range(i + 1, block_list):
if block[i] <= block[j]: # 물이 다 고였을 때
max_left = block[i]
max_right = block[j]
if max_right - max_left == 0: # 두개의 박스의 크기가 같을 때
for k in range(i + 1, j):
rain += max_right - block[k]
elif max_right > max_left: # 오른쪽에 있는 박스의 크기가 더 클 때
for k in range(i +1, j):
rain += max_left - block[k]
else:
pass
else: # a블록보다 b 블록이 크거나 같을 때 (물이 담길 수 없다면) = 시작할 수 없다면 !시작과 끝 지점에만 유효!
pass
return rain
print(raining([0, 1, 0, 1, 1, 0, 1, 3, 2, 1, 2, 1]))이게 첫번째로 만들었던 코드인데 내가 봤을 때는 정말 어디서 틀린건지도 모르겠다.
# 빗물을 담아보자 !
block_list = [0, 1, 0, 1, 1, 0, 1, 3, 2, 1, 2, 1]
block_len = len(block_list) - 1
rain = 0
for i in range(0, block_len):
if block_list[i] > block_list[i + 1]: # 빗물을 담을 수 있을 때
for j in range(i + 1, block_len):
if block_list[i] <= block_list[j]: # 빗물이 다 담겼을 때
high_left = block_list[i]
high_right = block_list[j]
print('i-index= ',i)
print('j-index = ',j)
print('i = ',block_list[i])
print('j = ',block_list[j])
if high_right - high_left > 0: # 오른쪽 벽이 더 크다면
for k in range(i + 1, j):
rain += high_left - block_list[k]
elif high_right - high_left < 0:
for k in range(i + 1, j):
rain += high_right - block_list[k]
else:
for k in range(i + 1, j):
rain += high_right - block_list[k]
else :
pass
else :
pass
print(rain)다음은 두번째 코드이다. 여기서 어디가 잘못되어서 실행결과가 이상한지 확인할 수 있었다. 이유는 j for문을 돌릴 때 i 보다 큰 값을 찾으면 바로 j가 i가 되어야 하는데( max_right의 값을 max_left에 담아야함) 그걸 하지 못한게 오류의 원인이라고 생각한다.
'Algorithm > 파이썬 알고리즘 인터뷰' 카테고리의 다른 글
| 파이썬 알고리즘 인터뷰 출처 (0) | 2022.07.11 |
|---|

댓글