트리구조의 관한 내용은 힙정렬때 간략하게 공부한 탓인지 쉽게 이해하고 넘어갈 수 있었다. 책의 마지막 부분이 가까워지니까 내용이 한번 봤던 내용이여서 그런지 전보다는 쉽게 공부하는 것 같다.
트리구조는 데이터 사이의 계층이 존재한다. 따라서 값의 크고작음이 구조 자체에 나타나기 때문에 정렬하는 방법도 쉽게 나타낼 수 있다.
트리구조
데이터간의 계층관계를 표현하는 자료구조
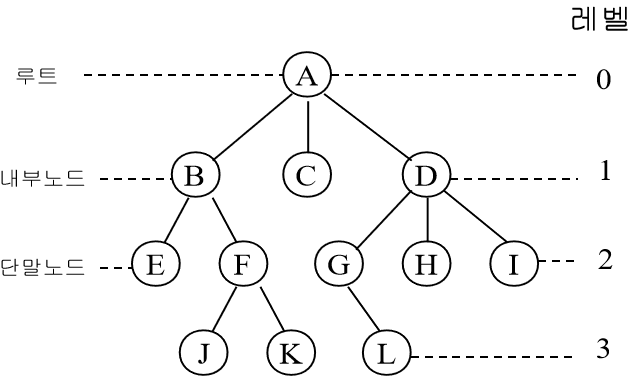
용어
루트 : 트리의 가장 위쪽에 있는 노드
리프 (단말 노드): 트리의 가장 아래쪽에 있는 노드
비 단말 노드 (내부노드): 리프를 제외한 노드
레벨 : 루트에서 얼마나 떨어져 있는지를 나타내는 것 가지가 아래로 뻗어나갈 때마다 레벨이 1씩 증가
차수 : 각 노드가 갖는 자식의 수
형제 : 부모가 같은 노드
순서 트리 : 형제 노드의 순서관계가 있는 트리
비 순서 트리 : 형제 노드의 순서관계가 없는 트리
순서 트리의 검색

너비 우선 검색 (BFS)
: 낮은 레벨부터 왼쪽에서 오른쪽으로 검색. 검색을 다 마쳤을 시에는 레벨을 증가시켜 검색
깊이 우선검색 (DFS)
: 리프에 도달할 때까지 아래로 내려가며 검색. 검색을 다 마쳤을 시에 부모노드로 돌아가며 다음 자식노드 검색
이진트리와 이진검색트리
힙 정렬의 대표적인 사용 예. 노드가 왼쪽 자식과 오른쪽 자식만을 가지며 두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관없음
→ 형제노드를 구분함
완전 이진 트리
루트로부터 아래쪽 레벨로 노드가 가득 차있고 같은 레벨 안에서 왼쪽부터 오른쪽으로 노드가 채워져 있는 이진 트리
→ 최대 노드의 수 : 2^(k + 1) - 1
다음은 트리 구조의 코드이다.
from __future__ import annotations
from typing import Any, Type
class Node:
def __init__(self, key, value, left, right):
self.key = key
self.value = value
self.left = left
self.right = right
class binary_search_tree:
def __init__(self):
self.root = None # 루트 초기화
def search(self, key):
p = self.root
while True:
if p is None:
return None
if key == p.key:
return p.value
elif key < p.key:
p = p.left
else:
p = p.right
def add(self, key, value):
def add_node(node, key, value):
if key == node.key:
return False
elif key < node.key:
if node.left is None:
node.left = Node(key, value, None, None)
else:
add_node(node.left, key, value)
else:
if node.right is None:
node.right = Node(key, value, None, None)
else:
add_node(node.right, key, value)
return True
if self.root is None:
self.root = Node(key, value, None, None)
return True
else:
return add_node(self.root, key, value)
def remove(self, key):
p = self.root
parent = None
is_left_child = True
while True:
if p is None:
return False
if key == p.key:
break
else:
parent = p
if key < p.key:
is_left_child = True
p = p.left
else:
is_left_child = False
p = p.right
if p.left is None:
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right
else:
parent.left = p.right
elif p.right is None:
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left
else:
parent.right = p.left
else:
parent = p
left = p.left
is_left_child = True
while left.right is not None:
parent = left
left = left.right
is_left_child = False
p.key = left.key
p.value = left.value
if is_left_child:
parent.left = left.left
else:
parent.right = left.left
return True
def dump(self):
def print_subtree(node):
if node is not None:
print_subtree(node.left)
print(f'{node.key} {node.value}')
print_subtree(node.right)
print_subtree(self.root)
def min_key(self):
if self.root is None:
return None
p = self.root
while p.left is not None:
p = p.left
return p.key
def max_key(self):
if self.root is None:
return None
p = self.root
while p.right is not None:
p = p.right
return p.key- 실행코드
from enum import Enum
from BinarySearchTree import binary_search_tree
Menu = Enum('Menu',['삽입','삭제','검색', '덤프', '키의범위', '종료'])
def select_Menu():
s = [f'({m.value}){m.name}'for m in Menu]
while True:
print(*s, sep = ' ', end='')
n = int(input(': '))
if 1 <= n <= len(Menu):
return Menu(n)
tree = binary_search_tree()
while 1:
menu = select_Menu()
if menu == Menu.삽입:
key = int(input('삽입할 키를 입력하시오 :'))
val = input('삽입할 값을 입력하시오 : ')
if not tree.add(key, val):
print('삽입에 실패했습니다 !')
elif menu == Menu.삭제 :
key = int(input('삭제할 키를 입력하시오 :'))
tree.remove(key)
elif menu == Menu.검색:
key = int(input('검색할 키를 입력하시오 :'))
t = tree.search(key)
if t is not None:
print(f'이 키를 갖는 값은 {t}입니다.')
else:
print('해당하는 데이터가 없습니다')
elif menu == Menu.덤프:
tree.dump()
elif menu == Menu.키의범위:
print(f'키의 최소값은 {tree.min_key()}입니다')
print(f'키의 최댓값은 {tree.max_key()}입니다')
else:
break'Algorithm > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| 원형 이중 연결 리스트 (0) | 2022.08.08 |
|---|---|
| 커서를 이용한 연결 리스트 (0) | 2022.08.07 |
| 포인터를 이용한 연결 리스트 (0) | 2022.08.05 |
| 문자열 검색 알고리즘 (0) | 2022.08.04 |
| 정렬 알고리즘 (fin) - 도수정렬 (0) | 2022.08.03 |
